|
|
匯文中學 |
學府雅苑 |
項王小區(qū) |
運河四橋 |
香格里拉 |
雙莊街東 |
三鼎集團 |
可成科技 |
金玉花園 |
科苑路處 |
|
00:00 |
0.372 |
0.347 |
0.344 |
0.387 |
0.338 |
0.364 |
0.344 |
0.370 |
0.282 |
0.375 |
|
01:00 |
0.373 |
0.349 |
0.347 |
0.388 |
0.340 |
0.367 |
0.348 |
0.375 |
0.284 |
0.380 |
|
02:00 |
0.368 |
0.347 |
0.344 |
0.383 |
0.338 |
0.367 |
0.346 |
0.374 |
0.282 |
0.380 |
|
03:00 |
0.367 |
0.348 |
0.346 |
0.381 |
0.342 |
0.367 |
0.353 |
0.378 |
0.283 |
0.384 |
|
04:00 |
0.377 |
0.358 |
0.366 |
0.391 |
0.362 |
0.376 |
0.375 |
0.385 |
0.296 |
0.391 |
|
05:00 |
0.383 |
0.366 |
0.374 |
0.398 |
0.369 |
0.393 |
0.389 |
0.413 |
0.303 |
0.417 |
|
06:00 |
0.373 |
0.350 |
0.347 |
0.396 |
0.346 |
0.391 |
0.375 |
0.425 |
0.286 |
0.430 |
|
07:00 |
0.352 |
0.324 |
0.312 |
0.379 |
0.319 |
0.371 |
0.385 |
0.421 |
0.259 |
0.428 |
|
08:00 |
0.341 |
0.319 |
0.302 |
0.375 |
0.309 |
0.363 |
0.371 |
0.414 |
0.251 |
0.418 |
|
09:00 |
0.336 |
0.315 |
0.297 |
0.368 |
0.304 |
0.359 |
0.363 |
0.404 |
0.246 |
0.409 |
|
10:00 |
0.336 |
0.310 |
0.282 |
0.370 |
0.288 |
0.353 |
0.321 |
0.396 |
0.237 |
0.403 |
|
11:00 |
0.342 |
0.315 |
0.290 |
0.373 |
0.295 |
0.358 |
0.332 |
0.405 |
0.242 |
0.411 |
|
12:00 |
0.351 |
0.309 |
0.284 |
0.375 |
0.291 |
0.355 |
0.330 |
0.400 |
0.239 |
0.405 |
|
13:00 |
0.349 |
0.321 |
0.299 |
0.370 |
0.303 |
0.360 |
0.335 |
0.399 |
0.250 |
0.405 |
|
14:00 |
0.349 |
0.333 |
0.317 |
0.372 |
0.318 |
0.369 |
0.348 |
0.407 |
0.263 |
0.412 |
|
15:00 |
0.351 |
0.330 |
0.314 |
0.373 |
0.316 |
0.368 |
0.343 |
0.399 |
0.261 |
0.405 |
|
16:00 |
0.350 |
0.330 |
0.313 |
0.371 |
0.315 |
0.373 |
0.343 |
0.404 |
0.260 |
0.409 |
|
17:00 |
0.345 |
0.327 |
0.308 |
0.371 |
0.313 |
0.369 |
0.344 |
0.410 |
0.256 |
0.415 |
|
18:00 |
0.352 |
0.328 |
0.308 |
0.375 |
0.313 |
0.375 |
0.348 |
0.416 |
0.256 |
0.421 |
|
19:00 |
0.353 |
0.330 |
0.311 |
0.374 |
0.315 |
0.377 |
0.352 |
0.416 |
0.258 |
0.422 |
|
20:00 |
0.353 |
0.329 |
0.313 |
0.374 |
0.318 |
0.380 |
0.355 |
0.420 |
0.258 |
0.426 |
|
21:00 |
0.360 |
0.334 |
0.319 |
0.380 |
0.323 |
0.382 |
0.357 |
0.418 |
0.263 |
0.423 |
|
22:00 |
0.367 |
0.343 |
0.339 |
0.385 |
0.341 |
0.388 |
0.374 |
0.424 |
0.277 |
0.429 |
|
23:00 |
0.378 |
0.351 |
0.353 |
0.394 |
0.351 |
0.369 |
0.366 |
0.385 |
0.289 |
0.389 |
|
離散程度 |
0.131 |
0.171 |
0.284 |
0.079 |
0.253 |
0.108 |
0.192 |
0.137 |
0.247 |
0.135 |
|
|
12月1日 |
12月2日 |
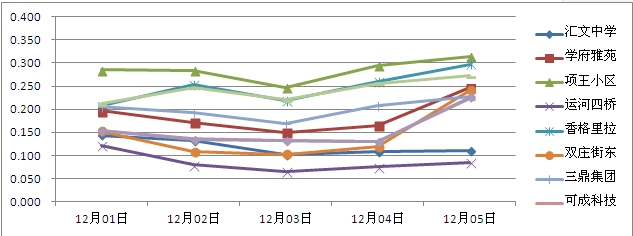
12月3日 |
12月4日 |
12月5日 |
平均離 散程度 |
|
匯文中學 |
0.143 |
0.131 |
0.101 |
0.108 |
0.110 |
0.119 |
|
學府雅苑 |
0.196 |
0.171 |
0.149 |
0.165 |
0.246 |
0.186 |
|
項王小區(qū) |
0.285 |
0.284 |
0.247 |
0.294 |
0.313 |
0.284 |
|
運河四橋 |
0.122 |
0.079 |
0.065 |
0.075 |
0.086 |
0.085 |
|
香格里拉 |
0.208 |
0.253 |
0.219 |
0.260 |
0.298 |
0.247 |
|
雙莊街東 |
0.152 |
0.108 |
0.102 |
0.118 |
0.241 |
0.144 |
|
三鼎集團 |
0.206 |
0.192 |
0.168 |
0.208 |
0.228 |
0.200 |
|
可成科技 |
0.154 |
0.137 |
0.132 |
0.131 |
0.224 |
0.156 |
|
金玉花園 |
0.212 |
0.247 |
0.220 |
0.256 |
0.272 |
0.241 |
|
科苑路處 |
0.155 |
0.135 |
0.133 |
0.129 |
0.226 |
0.156 |
